I've been in a terrible rut recently, and I figured the only way to get myself out of it is to publicly announce that I'll do something.
Skiplists it is. public declaration: I'm going to write a blog post titled "understanding and implementing skiplists" and publish it on the 1st of October, and It's going to be good! https://t.co/LQ5VhKqsx8
— Anirudh Rowjee @ override.bsky.social (@AnirudhRowjee) September 7, 2024
I gave myself 22 days to build a skiplist and write about it, so here we are. This is in no ways a perfect or even a good implementation; I've tried to be as hacky as possible, getting the bare minimum core functionality working while ignorning just about everything else.
You also have access to my C++ code1 and the original paper2, which contains most of the diagrams you'll see on this post. I've tried my level best to not look at other implementations before I implemented this, so the spirit of "implemented straight from the paper" is retained to a fair extent.
What are Skiplists?
A skiplist is a probabilistic, associative data structure based on linked lists. From a functionality point of view, it resembles a hashmap, or a dictionary. The best way to think about it is that it's an in-memory key-value store.
Formally, It allows the following operations (and you can swap out the strings for bytes, etc, any things that you can compare)
upsert(string key, string value)search(string key) -> optional<string value>scan(string start, string end) -> Vector<pair<string, string>>delete(string key)
How did we get here?
I have a bad problem with explaining everything - and though it makes for a good read, I'm trying to be more succinct so we can cover more stuff!
Consider the problem of searching over a set of keys - a collection, if you will. Attaching a value to the key is trivial.
The primitive linear search algorithm for almost any data structure (linked list, array, etc) is almost always O(n), which means it grows asymptotically at the same rate as the input. If we know all data beforehand, we can sort it, and then we can leverage algorithms such as binary search to give us O(log_2(n)) complexity, which work by successively reducing the search space by a factor of two (often at an additional O(n * log_2(n)) cost to sort the input).
Binary Search, Wikimedia Commons
However, we rarely know all inputs beforehand - we can't just dump the inputs in the order they came in, because that would break the sortedness invariant we have in order to achieve O(log_2(n)) complexity on search.
The ideal data structure then is something that supports maintaining the "sorted-ness" invariant with little interference from the user, and that also makes it easy to handle the following operations - insert, update, delete, scan - with relatively low asymptotic complexity.
The most ideal data structure for this task, and indeed, the choice of implementation for most languages and their standard implementations, is the Red-Black Tree, or some other form of self-balancing binary search trees. These data structures usually use a heuristic to approximate the "balanced-ness" of the tree - usually called balance factor - and often rely on complex rebalancing algorithms that must shuffle multiple pointers in place to accommodate for this.
Red-Black Tree, Wikimedia Commons
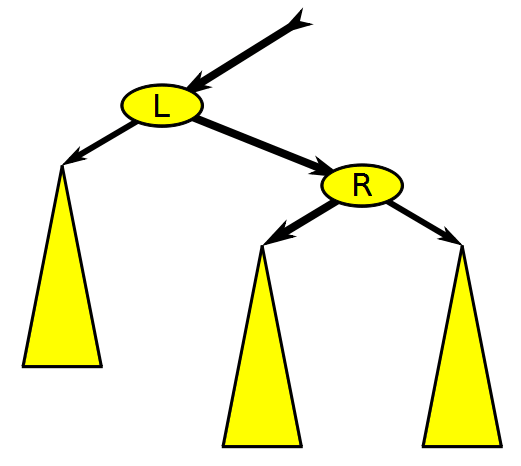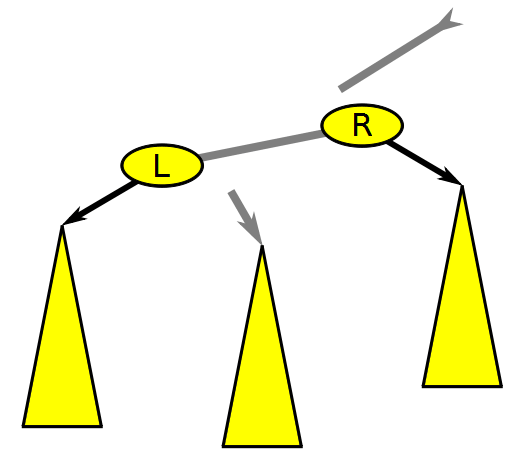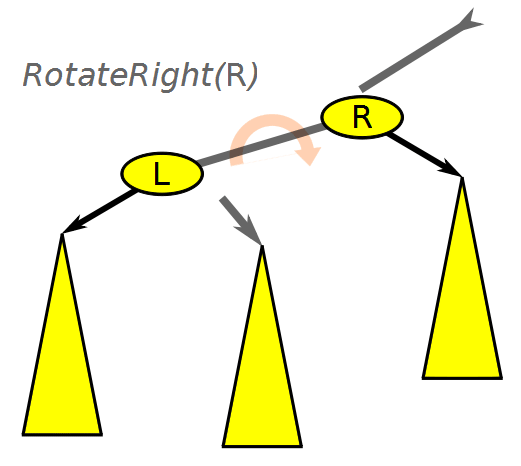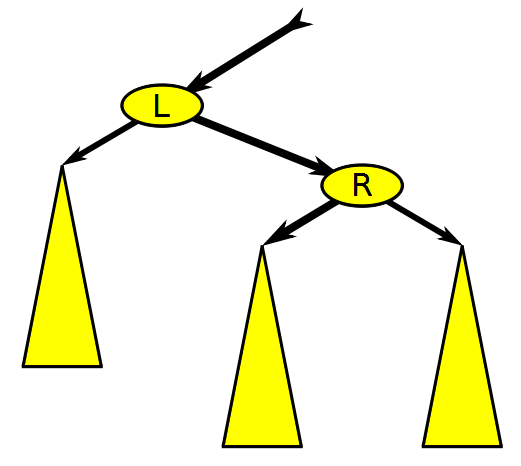Balanced Binary Search Tree Rotation, Wikimedia Commons
What if we could trade complexity for correctness? What if we could settle for an average case O(log(n)) with a worst case O(n), as opposed to the guaranteed average and worst case O(log(n)) with Binary Search? This is exactly the guarantee that skiplists make.
What does a skiplist look like?
Think of a singly linked list where each node has more than one pointers to other nodes organized in levels, where the highest level (say, 5) represents the largest number of nodes skipped, and the lowest level represents the lowest number (0) of nodes skipped (i.e. points to its immediate neighbour).
In this case, the 4th level connects every 8th node, the 3rd level connects every 4 nodes, the 2nd level connects every 2 nodes, and the 1st level connects every successive node.
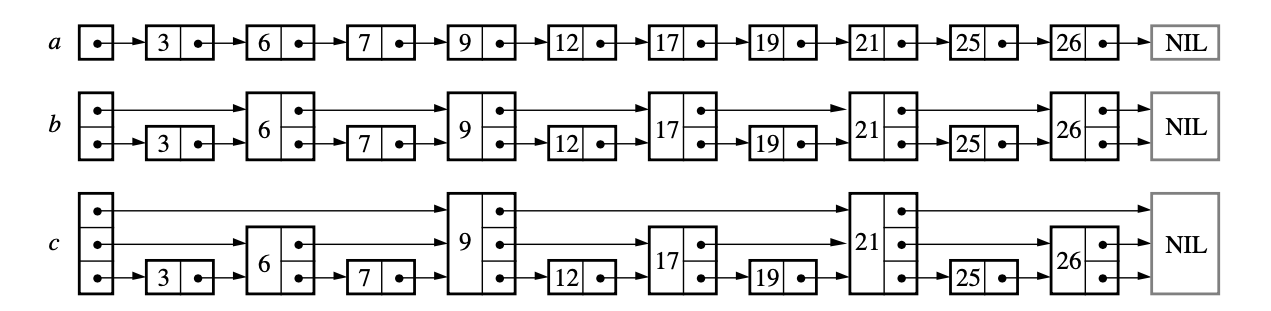Primitive example of a singly linked list with multiple forward pointers
A Skiplist can be thought of as a modification of a singly linked list that is maintained in sorted order, with the change that each node holds a fixed, randomly determined number of pointers to successive nodes, organized in the same paradigm of levels.
A Skiplist, from the paper
When we combine the sorted nature of the nodes in the a singly linked list (sorted by key, for example), and the idea of levels that allow you to skip some series of nodes, you start to see how it all falls into place; You can start at the highest level and make the largest jumps, successively reducing the search space as we move down the levels, and finally, arriving at the target node. This is a skiplist.
search(key k):
Start at the highest level
repeat until we are at the lowest level:
repeat until the next element key is greater than the search key
go to the next element
move down one level
An Intuition for Search
The best intuition I've heard for this is from Prof Srini Devas from MIT 6.046J3. In this case, we consider each node to be a subway/train station, and we consider pointers to be the train routes between them.
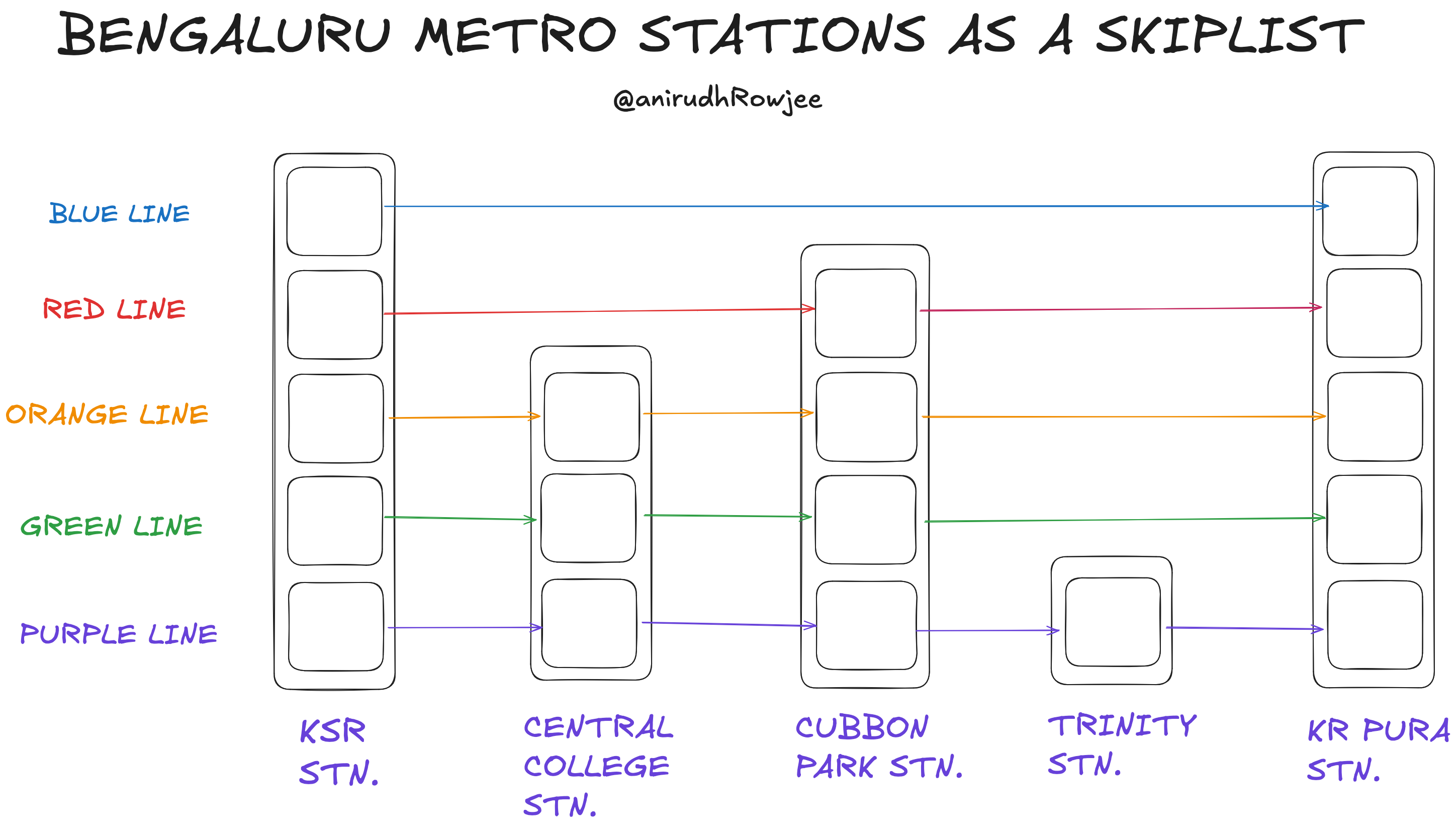The Purple Line of the Bengaluru Metro, made into a skiplist
In this scenario, we consider an arrangement of multiple rail lines (and thus, trains) plying between the same stations. Each station can have multiple trains!
Let us consider that the time taken to travel between any two stops is constant, regardless of how far they are. If I need to get from KSR Station to Central College Station, I am spoilt for choice; I have three train lines to choose from. If I want to get from KSR Station to Cubbon Park Station, I have two choices - I can either use the red line (no stops) or the orange, green, and purple lines (one stop). Clearly, the approach for the red line wins!
Lastly, consider a scenario where I have to go from KSR Station to Trinity Station. It might appear that the default path is 2 stops (KSR -> Central College -> Cubbon Park -> Trinity) - but in reality, I can do this in 1 stop by going from KSR -> Cubbon Park (via the red line), and then going from Cubbon Park -> Trinity (via the purple line). The key learning is that we can greedily adjust our strategy to have the least number of stops, provided that some sort of balance is maintained that doesn't negatively bias this whole process.
Who decides which lines connect which stations?
That's an extremely important question, and it's a critical part of what makes skiplists so successful. Keep that question in mind - this is also where probability comes into the picture.
The Math
As we discussed before, we rarely have all the data in our dataset present beforehand, which is why our skiplist must tolerate insertions, updates, and deletions, all while maintaining a reasonably low search complexity. In this reality, we can't assume that we know how many nodes there will be or where they'll be positioned, which is why deciding the level of a skiplist node is not trivial.
To ensure that, probabilistically, we have the highest change of skipping the most nodes in our search process, we must reduce the number of nodes in each level as we move from the lowest to the highest level. We can do this by
- Randomly setting the level of a node at insert time and
- controlling the rate of increase of the level of a node
To control the rate of increase, we use a fraction p - As Wikipedia puts it,
"... where an element in layer i appears in layer i + 1 with some fixed probability p"
And as the paper puts it,
"To get away from magic constants, we say that a fraction
pof the nodes with levelipointers also have leveli+1pointers."
Choosing p well is a matter of tuning, and the paper has some recommendations to make, given that it basically trades off space for accuracy.
The paper has a nice proof that fashions search instead as "climbing out of a list", and proves that search complexity is equal to O(log(n)). Wikipedia has a nice proof4 of the search cost being O(log(n)) as well.
Maintenance of a skiplist
Given that we understand that the skiplist is just an enhancement of a sorted linked list that has been augmented with more pointers, we see that every algorithm that modifies the skiplist (insertion, deletion, update) has the same rough structure:
mutate(skiplist):
find element to modify / insert after
update existing element OR create/delete the element
maintain the chain of pointers
The first two steps are rather straightforward: for 1, we use the search algorithm we just learnt about, and 2 is just memory allocation/deallocation.
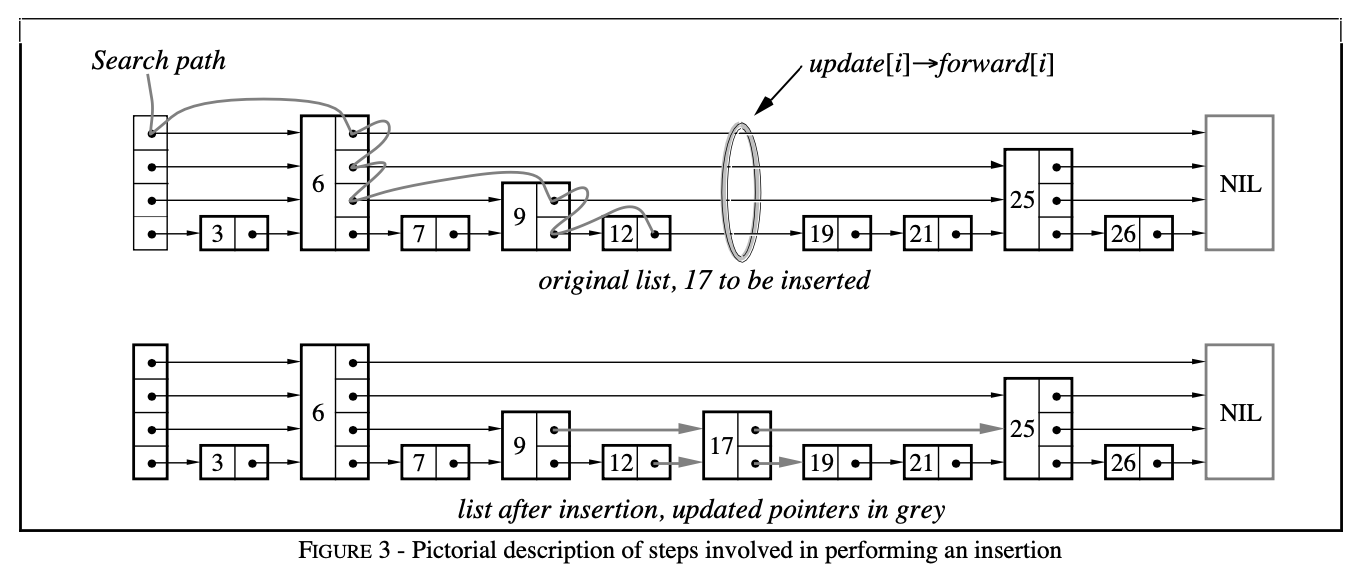
When it comes to pointer maintenance, we use a vector of pointers to the nodes right before the current node, called the update vector, to make our lives easier. The Update Vector holds all the predecessor nodes that will need to be updated if a new node is added, and allows us to maintain "pointer continuity" in that sense.
Advantages over other data structures
- Skiplists don't require expensive rebalance operations (see red-black trees)
- Skiplists make it very easy to do sequential scans on data (see red-black trees)
- Skiplists can be more easily modeled as concurrent data structures using atomic pointer operations 5
Implementing a skiplist
Fair warnings:
- Using
clangis frustrating sometimes. And Don't get me started onCMake. - The paper itself is 1-indexed, and I hope all your code is 0-indexed - this tripped me up for a while and caused some really funny segfaults, so be careful lol
- Everything in every class is
public- I know, this is very C-style programming, but I couldn't be bothered to write the appropriate accessors.
Defining the skiplist node
class SkiplistNode {
public:
std::vector<SkiplistNode *> links;
// Constructor
SkiplistNode(int current_level, std::string key, std::string value)
: current_level(current_level), key(std::move(key)),
value(std::move(value)) {
links = std::vector<SkiplistNode *>(current_level);
for (int i = current_level - 1; i >= 0; i--) {
links[i] = nullptr;
}
}
void DUMP() {
std::cout << fmt::format("SkiplistNode[{}] [{}:{}] AT {} ", current_level,
key, value, fmt::ptr(this))
<< std::endl;
for (int i = current_level - 1; i >= 0; i--) {
std::cout << fmt::format("\tNode at level {} pointing to {}", i,
fmt::ptr(links[i]))
<< std::endl;
}
}
int current_level;
std::string key;
std::string value;
};
Defining the Skiplist Class
I decided to explore std::optional<T> this time as a cure for my rust hangover; It works very nicely! the lack of a Result<T> equivalent made me sad but I hear that that's in the works too for C++23 with std::expected<T, E>. I've made up for this with std::pair<T, SkiplistError>, leading to some fairly go-like C++ code.
class SkiplistError {
public:
enum ErrorVariant { BAD_ACCESS, ALLOC_FAIL, KEY_NOT_FOUND, NOERR };
ErrorVariant e = ErrorVariant::NOERR;
std::string message;
SkiplistError(ErrorVariant e, std::string message = "")
: e(e), message(message){};
operator bool() { return e != NOERR; }
};
class Skiplist {
public:
// constructor
Skiplist(int max_level);
// Get the value associated with a particular key
std::optional<std::string> Search(std::string Key);
// Insert a key-value pair
std::pair<std::string, SkiplistError> Insert(const std::string &Key,
const std::string &Value);
// Delete a key and get the value associated with it on successful delete
std::pair<std::string, SkiplistError> Delete(std::string Key);
// Do a full scan of the skiplist
// TODO see if we can replace this with an iterator
std::pair<std::vector<std::pair<std::string, std::string>>, SkiplistError>
Scan();
// Find the point to insert a new skiplist node
std::pair<std::pair<SkiplistNode *, std::vector<SkiplistNode *>>,
SkiplistError>
identifyPredecessorNode(std::string key);
void DUMP();
~Skiplist();
SkiplistNode *START;
SkiplistNode *END;
int max_level;
int current_max_level;
// p: a tunable factor for the number of elements you want in the skiplist
float p;
std::mt19937 rng;
std::uniform_real_distribution<double> distribution;
int getRandomLevel();
};
Constructing a skiplist
This is the test that we wanted to pass:
TEST(SkiplistTest, test_init) {
// Initialize a Skiplist
const int max_level = 5;
auto sl = Skiplist(max_level);
for (int i = 0; i < max_level; i++) {
ASSERT_EQ(sl.START->links[i], sl.END);
}
}
and here's the constructor:
Skiplist::Skiplist(int max_level) : max_level(max_level) {
p = 0.5;
rng = std::mt19937(std::time(nullptr)); // fixed seed as of now
distribution = std::uniform_real_distribution<double>(0.0, 1.0);
// Initialize the sentinel nodes
START = new SkiplistNode(max_level, "START_KEY", "START_VALUE");
END = new SkiplistNode(max_level, "END_KEY", "END_VALUE");
// Connect the start and end nodes
for (int i = 0; i < max_level; i++) {
START->links[i] = END;
}
}
Here, START and END are special nodes, which are the sentinel nodes of the skiplist. In all honesty, it would probably be "cleaner" to use a nullptr to terminate the node pointers, but I felt like having a dedicated END node would be a better option. This would also help maintain the invariant that there will never be a nullptr in the search path, as we will see later.
Implementing Insertion
Given that insertion and search are two really tightly coupled algorithms (you need search to implement insertion, but you also need insertion to be able to test search?), I was forced to implement both at once.
Here's the test we wanted to pass (and there's another one that tests search later as well).
TEST(SkiplistTest, test_insert) {
auto linear_search = [](std::string key,
Skiplist *sl) -> SkiplistError::ErrorVariant {
auto curr_node = sl->START;
while (curr_node != sl->END) {
if (curr_node->key == key) {
return SkiplistError::ErrorVariant::NOERR;
} else {
curr_node = curr_node->links[0];
}
}
return SkiplistError::ErrorVariant::KEY_NOT_FOUND;
};
// Check the monotonicity of the keys
auto monotonicity_check = [](Skiplist *sl) -> SkiplistError::ErrorVariant {
auto currentNode = sl->START->links[0];
std::string prevText = "";
std::string currentText = "";
while (currentNode != sl->END) {
prevText = currentText;
currentText = currentNode->key;
if (!(currentText > prevText)) {
return SkiplistError::BAD_ACCESS;
}
currentNode = currentNode->links[0];
}
return SkiplistError::ErrorVariant::NOERR;
};
const int max_level = 5;
std::cout << fmt::format("initializing skiplist with level {}", max_level)
<< std::endl;
auto sl = new Skiplist(max_level);
std::vector<std::tuple<std::string, std::string>> kvPairs = {
{"hello", "world"}, {"something", "else"},
{"enter", "sandman"}, {"the struts", "could have been me"},
{"hello", "world2"}, {"END_KEY", "SYSTEM BROKEN!!!"}};
for (auto [key, value] : kvPairs) {
// Insert an element and search for it
auto [retval, err] = sl->Insert(key, value);
ASSERT_EQ(err.e, SkiplistError::NOERR);
sl->DUMP();
// Do a simple linear search
ASSERT_EQ(linear_search(key, sl), SkiplistError::NOERR);
// Ensure that monotonicity is maintained
ASSERT_EQ(monotonicity_check(sl), SkiplistError::NOERR);
}
}
Here's the insertion code, beginning with identifying the predecessor node. This code is common across all mutating functions, and will be reused in other places, so I've made it a function of its own; it returns the pointer to the predecessor node or the node itself, and the update vector of nodes that we used to reach the predecessor node.
std::pair<std::pair<SkiplistNode *, std::vector<SkiplistNode *>>, SkiplistError>
Skiplist::identifyPredecessorNode(std::string key) {
// Initialize the update vector
auto update = std::vector<SkiplistNode *>(max_level, nullptr);
// See if the node already exists
auto current_node = START;
auto next_node = START;
auto max_search_level = max_level - 1;
for (int i = max_search_level; i >= 0; i--) {
// Check if the next node in the level has a key that comes before our
// search key
// See if the next node is a sentinel element
next_node = current_node->links[i];
while (next_node->key < key && next_node != END) {
current_node = next_node;
next_node = current_node->links[i];
}
update[i] = current_node;
}
current_node = current_node->links[0];
return std::make_pair(std::make_pair(current_node, update),
SkiplistError(SkiplistError::ErrorVariant::NOERR));
}
And finally, the insertion code itself:
// This is called insert but it has upsert semantics
std::pair<std::string, SkiplistError>
Skiplist::Insert(const std::string &key, const std::string &value) {
// Figure out where to insert the node: this is either the node with the same
// key, so we can update the value, or we found the node right before the
// insertion point so that we can insert after it
auto [meta, error] = identifyPredecessorNode(key);
if (error.e != SkiplistError::NOERR) {
return std::make_pair("", error);
}
std::cout << "Predecessor Found!" << std::endl;
auto [current_node, update] = meta;
if (current_node->key == key) {
// If the key exists at the current node, update its value
std::cout << fmt::format("BAZINGA! Key {} found with value {}",
current_node->key, current_node->value)
<< std::endl;
auto oldVal = current_node->value;
current_node->value = value;
return std::make_pair(value, SkiplistError::NOERR);
} else {
// If they key doesn't exist at the current node, insert it
std::cout << "Node not found" << std::endl;
// The node doesn't exist;
// Construct a new node
int level = getRandomLevel();
// WARN
// Not doing this rn: need to update the max level of the list if this
// happens I doubt it will but the paper says we need to do it so ¯\_(ツ)_/¯
if (level > max_level) {
}
auto new_node = new SkiplistNode(level, key, value);
for (int i = 0; i < level; i++) {
new_node->links[i] = update[i]->links[i];
update[i]->links[i] = new_node;
}
// Update all the pointers in the reachability chain to reach this node
return std::make_pair(value, SkiplistError::NOERR);
}
}
As we discussed before, the level of a new skiplist node is governed by a random number generator. The p factor here is extremely crucial to the "balancing" of your skiplist;
int Skiplist::getRandomLevel() {
int level = 1;
while ((distribution(rng) < p) && (level < max_level)) {
level += 1;
}
return level;
}
Implementing Search
Test to pass:
TEST(SkiplistTest, test_insert_and_search) {
const int max_level = 5;
std::cout << fmt::format("initializing skiplist with level {}", max_level)
<< std::endl;
auto sl = Skiplist(max_level);
sl.DUMP();
// Load some data into the skiplist
std::vector<std::tuple<std::string, std::string>> kvPairs = {
{"hello", "world"},
{"something", "else"},
{"enter", "sandman"},
{"martin garrix", "under pressure"},
{"the smiths", "please please please let me get what I want"},
{"the struts", "could have been me"},
{"hello", "world2"}};
for (auto [key, value] : kvPairs) {
auto [retval, err] = sl.Insert(key, value);
ASSERT_EQ(err.e, SkiplistError::NOERR);
}
// Search for elements in the skiplist
std::vector<std::tuple<std::string, std::optional<std::string>>> testcases = {
{"something", "else"},
{"enter", "sandman"},
{"the struts", "could have been me"},
{"martin garrix", "under pressure"},
{"this isn't there", std::nullopt},
{"the smiths", "please please please let me get what I want"},
{"hello", "world2"},
{"nonexistent", std::nullopt}};
for (auto [key, searchResult] : testcases) {
ASSERT_EQ(sl.Search(key), searchResult);
}
}
And the algorithm, most of which has been taken from the identifyPredecessorNode function, both of which are based on the paper:
std::optional<std::string> Skiplist::Search(std::string Key) {
std::cout << "Searching for -> " << Key << std::endl;
auto current = START;
auto max_search_level = max_level - 1;
for (int i = max_search_level; i >= 0; i--) {
while (current->links[i]->key < Key && current->links[i] != END) {
std::cout << fmt::format("Exploring key -> {}", current->links[i]->key)
<< std::endl;
current = current->links[i];
}
}
current = current->links[0];
if (current->key == Key) {
return std::optional<std::string>{current->value};
} else {
return std::nullopt;
}
}
Implementing Delete
This also followed the same pattern as the insert operation as before, just that it now frees memory as well as deleting everything else.
Here is the test we need to pass:
TEST(SkiplistTest, test_delete) {
const int max_level = 5;
std::cout << fmt::format("initializing skiplist with level {}", max_level)
<< std::endl;
auto sl = Skiplist(max_level);
// Load some data into the skiplist
std::vector<std::tuple<std::string, std::string>> kvPairs = {
{"hello", "world"},
{"something", "else"},
{"enter", "sandman"},
{"martin garrix", "under pressure"},
{"the smiths", "please please please let me get what I want"},
{"the struts", "could have been me"},
{"hello", "world2"}};
for (auto [key, value] : kvPairs) {
auto [retval, err] = sl.Insert(key, value);
ASSERT_EQ(err.e, SkiplistError::NOERR);
}
// Delete some elements
std::vector<std::tuple<std::string, SkiplistError::ErrorVariant>> testcases =
{{"hello", SkiplistError::NOERR},
{"enter", SkiplistError::NOERR},
{"this will break", SkiplistError::KEY_NOT_FOUND}};
for (auto [key, err] : testcases) {
std::cout << fmt::format("Deleting {}", key) << std::endl;
auto [retval, reterr] = sl.Delete(key);
sl.DUMP();
ASSERT_EQ(reterr.e, err);
}
}
And here's the implementation:
std::pair<std::string, SkiplistError> Skiplist::Delete(std::string Key) {
std::string oldVal;
// Figure out where to delete the node: this is either the node with the same
// key, so we can update the value, or we found the node right before the
// insertion point so that we can insert after it
auto [meta, error] = identifyPredecessorNode(Key);
if (error.e != SkiplistError::NOERR) {
return std::make_pair("", error);
}
auto [nodePtr, update] = meta;
if (nodePtr->key == Key) {
// We have found the right node to delete
// update all the necessary pointers
for (int i = 0; i < max_level; i++) {
if (update[i]->links[i] != nodePtr) {
break;
}
update[i]->links[i] = nodePtr->links[i];
}
oldVal = nodePtr->value;
delete nodePtr;
// TODO update overall list level
return std::make_pair(oldVal,
SkiplistError(SkiplistError::ErrorVariant::NOERR));
} else {
return std::make_pair(
"", SkiplistError(SkiplistError::ErrorVariant::KEY_NOT_FOUND));
}
return std::make_pair("",
SkiplistError(SkiplistError::ErrorVariant::BAD_ACCESS));
}
}
Implementing Scan
This one is pretty simple. We only need to read all key-value pairs into an array. There's probably a better way of doing this, but this will suffice for now.
The test we want to pass:
TEST(SkiplistTest, test_fullscan) {
const int max_level = 5;
std::cout << fmt::format("initializing skiplist with level {}", max_level)
<< std::endl;
auto sl = Skiplist(max_level);
// Load some data into the skiplist
std::vector<std::pair<std::string, std::string>> kvPairs = {
{"something", "else"},
{"enter", "sandman"},
{"martin garrix", "under pressure"},
{"the smiths", "please please please let me get what I want"},
{"the struts", "could have been me"},
{"hello", "world2"}};
for (auto [key, value] : kvPairs) {
auto [retval, err] = sl.Insert(key, value);
ASSERT_EQ(err.e, SkiplistError::NOERR);
}
// Copy over the kv pairs
std::vector<std::pair<std::string, std::string>> kvPairsSorted = kvPairs;
std::sort(kvPairsSorted.begin(), kvPairsSorted.end(),
[](std::pair<std::string, std::string> &a,
std::pair<std::string, std::string> &b) -> bool {
return std::get<0>(a) < std::get<0>(b);
});
std::cout << "Printing out sorted list: " << std::endl;
for (auto k : kvPairsSorted) {
std::cout << fmt::format("Key {} Value {}", std::get<0>(k), std::get<1>(k))
<< std::endl;
}
auto [res, err] = sl.Scan();
ASSERT_EQ(err.e, SkiplistError::NOERR);
ASSERT_EQ(res, kvPairsSorted);
}
and here's the implementation:
std::pair<std::vector<std::pair<std::string, std::string>>, SkiplistError>
Skiplist::Scan() {
std::vector<std::pair<std::string, std::string>> answer = {};
auto current_node = START->links[0];
while (current_node != END) {
answer.push_back(std::make_pair(current_node->key, current_node->value));
current_node = current_node->links[0];
}
return std::make_pair(answer, SkiplistError(SkiplistError::NOERR));
}
Destructor
There has to be a better way to do this, but I wanted to be safe.
Skiplist::~Skiplist() {
std::cout << "Destructing Skiplist" << std::endl;
auto [res, err] = Scan();
if (err.e != SkiplistError::NOERR) {
} else {
for (auto [k, _] : res) {
auto [res1, err1] = Delete(k);
if (err1.e != SkiplistError::NOERR) {
std::cout << fmt::format("Failed to delete key {}", res1) << std::endl;
}
}
}
}
Notes
- you can find the code for
DUMP, as well as the CMakeLists.txt file on Github. - My rule of not looking at another implementation might have harmed me more than it helped me!
- only a few null pointers were harmed in the making of this post.
Acknowledgements
I'd really like to thank Phil Eaton, whose practice of writing monthly technical blog posts has been a long-standing inspiration of mine, and thanks to whose encouragement this blog post exists.
I would also like to thank Navin Shrinivas for being my accountability buddy throughout this process, and Achyut Yogesh Sosale, Kiran Rajpurohit, Siddarth Tewari, and Anirudh Sudhir for their suggestions on how I could make this post better. Thank you folks so, so much!
And lastly, to everyone on twitter who has been listening along on my journey and supporting me with encouraging comments and feedback - thank you!
And thank you, dear reader, for reading :D if you have any feedback (suggestions, comments, corrections), you can find me on twitter or email.